This is the second in a series of posts about Locke’s theory of space.

At the end of the previous post, I had posed the question, how the combination of two simple ideas — namely, the ideas of space and of limit or finitude — can yield, rather than a single mixed mode, an infinite number of distinct simple modes. I began my answer by saying that the idea of finitude, in this case, given what Locke takes to be its empirical origin, is the idea of what is left behind when a part of body moves away from another part. Or, as I also put it: the “obvious portions of extension” can affect us with the idea of a finite empty space because of the divisibility of body. I pointed out, however, that this explanation addresses directly only the question of quantitative diversity of our ideas of spaces: these can be of any size, relative to one another, because body is infinitely divisible. What is less clear is how to explain their specific qualitative diversity: why, although they can be of infinitely many different shapes, there are tight constraints on what these shapes may be (e.g. the so-called triangle postulate, which requires that the interior angles of a triangle be equal to two right angles).

Figure 1: New superficies where before there was a continuity.

To begin dealing with this latter problem, let’s take a closer look at the process of division, which, recall, Locke defines as “by removing the Parts one from another, to make two Superficies, where before there was a Continuity” (2.13.13) (fig. 1). As the new superficies \(TK\) moves away from the new superficies \(HX\), \(T\) moves along a line \(BA\) which passes through \(H\), while \(K\) moves along a second line \(DZ\) which passes through \(X\). I have drawn both the lines \(BA\) and \(DZ\) as straight[1]×Locke, along with most geometers throughout the Western history of the subject, uses “line” to mean something which may (or perhaps must) be of finite length and which may be either straight or curved. In other words, this is roughly what we now call a “curve,” although it probably is not helpful to think of it as a set of points parameterized by an interval of the real numbers. For Locke, then, “straight line” is not a pleonasm. because that evidently is how Locke thinks of them, but also because it helps bring out the similarity between this figure and two other figures which I will now proceed to discuss.

Figure 2: The sucker in a pump. Detail from a diagram of Boyle’s third air-pump. Credit: Wellcome Collection. Attribution 4.0 International (CC BY 4.0). Accessed on Wikimedia Commons.

The first (fig. 2) shows something Locke mentioned in a passage I quoted in my previous post: the sucker of a pump. Specifically, it shows a sucker in the third of the famous air pumps constructed by Robert Boyle. Locke was part of Boyle’s circle in his Oxford years, so it makes sense that, when he thinks about an empty space, he thinks about a body being divided in this particular way: one piece sliding away from the other so as to leave behind a space which, if no other body moves into it, will remain empty. That the case of a perfect vacuum pump is at least conceivable shows, according to Locke, that our general idea of the process of division involves no supposition about the existence of any other bodies, although, obviously, if there are any other bodies around, their motions must be such as not to resist it. Somehow, from the mere idea of the original body, together with the ideas of the two pieces formed from it, we can understand that this process is possible.

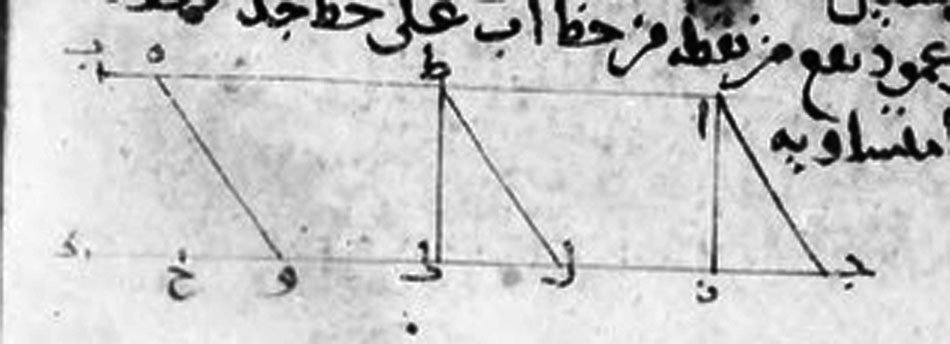
Figure 3: MS Paris Bibliothèque Nationale arabe 2457, detail of fol. 157v. Source gallica.bnf.fr / Bibliothèque nationale de France.

The second (fig. 3) is perhaps a bit more unexpected. This diagram comes from one of the two proofs of Euclid’s parallel postulate due to Thābit ibn Qurra.[2]×For a printed version of this text, with French translation, see R. Rashed and C. Houzel, “Thābit ibn Qurra et la théorie des parallèles,” Arabic Sciences and Philosophy 15 (2005):9–55 (available online here for those who have access); I will quote from their printed text, since I can’t easily read the manuscript. For an English translation see A.I. Sabra, “Thābit Ibn Qurra on Euclid’s Parallels Postulate,” Journal of the Warburg and Courtauld Institutes 31 (1968):12–32. I learned of this work from De Risi, to be cited below. The diagram pertains to Thābit’s proof of his first lemma, namely:

Any two straight lines which are in one plane, and there go out through what is between them two [further] straight lines that meet [the first two], and [these second two lines] are equal and contain with one of the first two lines equal angles on one side: any two perpendiculars which fall on that line from two points of the other line [of the first two] are equal. (Rashed and Houzel, p. 29, ll. 11–14)

Figure 4: My version of Thābit’s figure.

That is (fig. 4): if, for example, between the straight lines \(AB\) and \(GD\), one can draw two equal straight lines \(HW\) and \(AG\) such that \(\angle \,HWD = \angle \,AGD\), then all lines like \(TK\) — straight lines drawn between a point \(T\) on \(AB\) and a point \(K\) on \(GD\), and perpendicular to \(GD\)[3]×In Euclidean geometry, it will, of course, also follow that \(TK\) is perpendicular to \(AB\), since the hypothesis is sufficient to show that \(AB\) and \(GD\) are parallel. But Thābit does not assume that, since the proof of it would depend on the parallel postulate that he is trying to establish. — are equal to one another. For the purposes of the proof, Thābit introduces (though he makes this explicit only later on) auxiliary points \(Z\) and \(X\), defined as the points of intersection with \(DG\) of perpendiculars dropped from \(A\) and \(H\), respectively.[4]×That we can do this is guaranteed by Elements 1.12, which is independent of the parallel postulate. He then begins:

We imagine [نتوهمnatawahham] that a solid contains the line \(AG\) and the segment \(GZ\) of the [straight] line \(GD\), such that they are within it, and that that solid moves, in its entirety, from the side of \(G\) to the side of \(D\), by one straight simple motion, along the direction [استقامةistiqama] of the line \(GD\), and that, moreover, there is the like of the lines \(AG\), \(GZ\) drawn in it, remaining in it, with [shapes] like their shapes. (Rashed and Houzel, loc. cit., ll. 19–22)

He then proceeds to show that, as the solid carries the triangle \(AGZ\) (or its “like,” مثالmithal — Sabra translates “analog,” which is loose but not unreasonable) along, the line \(GZ\) will move along \(GD\) until eventually \(G\) coincides with \(W\) and \(Z\) coincides with \(X\), and that, at that time, \(A\), having moved along the straight line \(AB\), will coincide with \(H\). On this basis he is able to show that, as \(A\) passes through any random point \(T\) on \(AB\), \(Z\) will pass through the intersection \(K\) with \(GD\) of the perpendicular dropped from \(T\). Hence any such perpendicular \(TK\) is equal to \(AZ\), and so they are all equal to one another, QED.

If you look in Vincenzo De Risi’s informative introduction to his edition of Sachheri’s Euclides vindicatus,[5]×Gerolamo Saccheri, Euclid Vindicated from Every Blemish, ed. V. De Risi, tr. G.B. Halsted and L. Allegri (Birkhäuser, 2014); ISBN 978-3319059655. you will find Thābit described as “arguably, the creator” of a proof of the parallel postulate “from motion,” which De Risi describes as follows:

Beginning in the Middle Ages, there was yet another hurdle: the incorrect but very tempting argument involving the employment of motion in geometry. Let the end point of a line segment slide continuously along a straight line, and let the segment remain perpendicular to the line while moving: then the other end point will trace out a line, undoubtedly equidistant from the given straight line; and it was evident to all that the line generated in this way could not be other than a straight line itself. . . .  For many centuries the genetic character of this procedure deceived countless mathematicians, who could not explain how such a simple and uniform movement might generate a curve — in fact, it would be hard for anyone lacking an account of curvature, that is, anyone before Gauss, to provide such an explanation. (p. 9; the description of Thābit as “arguably, the creator” is in n. 9 there)

But, although this bit of ultra-whig history may well apply to the later versions of the proof, for example the versions of Clavius and Borelli that are criticized by Saccheri, it does not apply to Thābit’s (arguably) original version. For, first of all, Thābit assumes, not that a line (segment) is moving, but that a solid is moving, and carrying a triangle along with it. True, he does seem to indicate, in his introductory remarks, that the use of a solid is strictly unnecessary, and to envision, therefore, a proof more along the lines of Clavius’ or Borelli’s. But he refrains from taking that course because to imagine this kind of motion of a line along another line would be, he says, “an unfamiliar thing,” and “it is not certain but that the line, in its transport [نقلةnuqla],[6]×Forms of this root, نقلn-q-l, are, at least today, the (Modern Standard Written) Arabic equivalents for English “transport” or “transportation” (although نقلةnuqla apparently now means “migration”). Such present day equivalences often have their roots in medieval translation traditions, and I would like to think it no coincidence that Thābit uses the term here in what is (arguably) history’s first discussion of parallel transport. The latter expression (for which, I see towards the bottom of this page, the current Arabic is indeed نقل متوازيnaql mutawaziy), originates, I believe, with Tullio Levi-Civita, “Nozione di parallelismo in una varietà qualunque e conseguente specificazione geometrica della curvatura riemanniana,” Rendiconti del Circolo Matematico di Palermo 42 (1917):173–215, reprinted in his Opere matematiche. Memorie e note (Bologna: Nicola Zanichelli, 1954–75) 4:1–39, where the phrase “il trasporto di direzioni parallele lungo una qualsiasi curva” occurs on p. 3. Moreover, I note that Levi-Civita had an early interest in classical languages, and that his high school mathematics teacher, the number theorist Paolo Gazzaniga, recalled that his precocious student produced “an attempted demonstration of the parallel postulate that ran, elegant and impeccable, up to an inadvertent final admission, in which the petitio principii was nestled” (U. Amaldi, “Tullio Levi-Civita,” in Levi-Civita, Opere, 1:ix-xxx, p. x). (I owe both of these references to Iurato and Ruta, to be cited below. My knowledge of Italian consists entirely of half-remembered high school Spanish, assisted by Google Translate.) Nevertheless, I don’t know how to supply any of the missing steps between Thābit and Levi-Civita, and it’s quite possible that نقلةnuqla here should be rendered “translation.” Thābit, presumably, is not thinking of the distinction between segments in the underlying space and vectors in the tangent bundle that would decide which he means, and meanwhile نقلةnuqla can be used for φοράphora, e.g. at Top. 4.2.122b27 (Arabic here), where Boethius (PL 64:945A) has latio. might change its shape or position,” and so he instead begins with “a well-known thing which I have premised concerning the solid,” namely with the following:

For any solid that we imagine to be moved in its entirety to one side by one simple direct motion: any point of it will be moved directly, and will delineate in its passage a straight line along which it passes, and as for the straight lines that are in [the solid], those of them that are in the direction of its motion will also pass along a straight line, whereas those of them that are in other than the direction of its motion will not do so. (Rashed and Houzel, loc. cit., ll. 5–9)

Following what seems to be the tradition in this field (historiography of the parallel postulate), we might call this “Thābit’s axiom.” Although the motivation he offers for it may be a little difficult to follow, the axiom itself is clear enough, and he applies it in his proof to show exactly what, according to De Risi, generations of mathematicians couldn’t bring themselves to doubt: namely, that the point \(A\) traces a straight line as it moves.

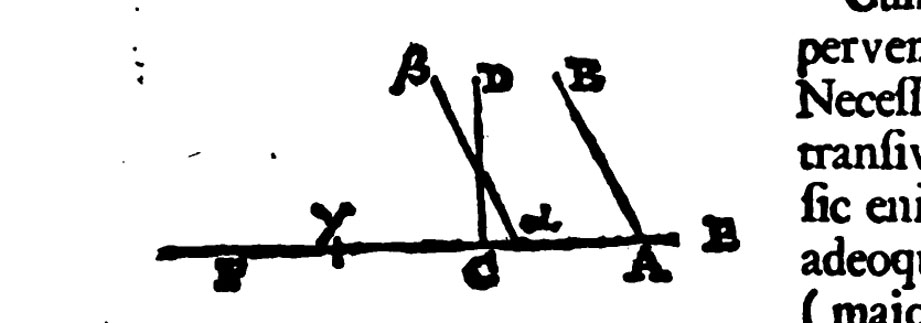
Figure 5: The line (segment) \(\alpha \beta \) starts out coincident with \(AB\) and moves left along \(EF\) until \(\alpha \) coincides with \(C\). From Wallis, De algebra, p. 676.

But could Locke possibly have known anything about this text, which is extant in only two manuscripts, and which did not appear in print until the 20th century? Somewhat surprisingly, the answer is that he could have. Not that he likely read an obscure Arabic manuscript himself: although he was required to attend lectures on the Arabic language as part of his senior studentship at Christ Church, I have no reason to think[7]×Based on my usual half-ass research. that he ever became very competent at it. The man who gave those lectures, however, Edward Pococke (or Pocock), was Locke’s favorite professor at Oxford. And we know that Pococke, around this time, was collaborating with another teacher of Locke’s, John Wallis (also a close associate of Boyle’s and his fellow adversary of Hobbes), in the study of Arabic proofs of the parallel postulate. At any rate, when Wallis later published his own proof,[8]×In De postulato quinto et quinta definitione libri 6 Euclidis disceptatio geometrica, an appendix to Wallis’s De algebra tractatus (Oxford, 1693). The main book is a Latin version of Wallis’s 1685 Treatise of Algebra, but this appendix is based on a lecture that he delivered on July 11, 1663, i.e. while Locke was still at Oxford. he published it along with Pococke’s Latin translation of another medieval Arabic proof, this one due to the great Persian polymath Naṣīr al-Dīn al-Ṭūsī.[9]×The published proof is now thought, on what evidence I don’t know, to be actually the work of a disciple. But Pococke also translated and shared with Wallis a version still thought to have been written by al-Ṭūsī himself: see De Risi, Introduction to Euclid Vindicated, p. 10 n. 12 and p. 16 n. 23. There is, moreover, some indication that Pococke might have shared knowledge of a different manuscript work of Thābit’s with Wallis. This is highly conjectural, but: (1) Pococke spent three years in Constantinople in the late 1630’s, collecting books and studying rare manuscripts; (2) MS 4832 of the Library of Aya Sofya Museum in Istanbul contains a letter in which Thābit states, without proof, a certain generalization of the Pythagorean theorem; (3) the final three chapters of Wallis’s Treatise of Angular Sections, which were composed in 1665, are based on what is effect the same result.[10]×See C.J. Scriba, “John Wallis’ Treatise of Angular Sections and Thâbit ibn Qurra’s Generalization of the Pythagorean Theorem,” ISIS 57 (1966), pp. 56–66. Scriba himself does not actually assert, or even conjecture, that Wallis knew of Thābit’s work, though, thanks to a misreading of his paper in G.G. Joseph, The Crest of the Peacock: Non-European Roots of Mathematics (Penguin, 1990, ISBN 978-0691135267), p. 337, he has ended up as the indirect source of this assertion in the Wikipedia article on Wallis (and, in case it isn’t obvious: it is by following that same trail in the other direction that I arrived at Scriba’s article). Note that the same manuscript, Aya Sofya 4832, also happens to contain one of the extant copies of Thābit’s other proof of the parallel postulate. Finally, and most suggestively, Wallis’s own proof of the parallel postulate, although based on a different principle (now known, of course, as “Wallis’s axiom”), does nevertheless involve a segment transported along a straight line from one position to another, and so still contains a version of our same familiar picture (fig. 5). So there is at least some possibility that Pococke and Wallis knew of Thābit’s proof, and, if they did, Locke might well have heard about it from one or both of them.

I don’t think it necessary to insist that he did, however. The main point is what Thābit’s procedure — what the correctness of his procedure — shows about the relationship between the motion of bodies and the possible simple modes of space. For there is no error in Thābit’s proof, or, at least, no mathematical error, but there is a reason De Risi takes it for granted that there must be one: namely, that, as we now know, non-Euclidean geometries are possible. Since a proof of the parallel postulate amounts to showing that, at least in one important sense, a non-Euclidean geometry is not possible, it is natural to suspect that any such proof must contain an error.

What is it, however, that we know, under the title “that non-Euclidean geometry is possible”? This is actually one of those simple questions that gets harder and harder to answer the more carefully you think about it. One way to get at the problem is to imagine that two people are disputing: A maintains that Euclid is right about geometry, while B says that Euclid is right except insofar as his system depends on the parallel postulate, which, according to B, is false. From the point of view of contemporary (“pure”) mathematics (a point of view originally stemming, in large part, from the acceptance of non-Euclidean geometry), it may seem difficult to understand what A and B could be arguing about. Euclid is “right” about his geometry — that is, his theorems are consequences of his axioms[11]×Plus some additional axioms which he doesn’t state. — but he is not, obviously, “right” about some other geometry — that is, not all his theorems are consequences of some other set of axioms. Isn’t that the end of matter? But there is still one way a contemporary mathematician can understand the dispute: namely, if we assume that A thinks B’s position is inconsistent, and vice versa. The consequences of an internally inconsistent set of axioms are not worth studying. The hero of our story, considered in this light, will be Eugenio Beltrami, who showed, in 1868, that B’s system (what we now call “hyperbolic geometry”) is consistent if and only if A’s is. It follows that neither A nor B will be able to win the debate on these terms.

If we see the history of thought on this question, up until the time of Gauss, Lobachevsky, and Bolyai, as a misguided attempt to stave off one half of Beltrami’s breakthrough, or, in other words, as one long attempt on A’s part to find a contradiction in B, then it will be evident that every proof produced during that history must involve an error of one kind or another. Either A must commit some actual sophism, or A must have induced B to accept some extra assumption that goes beyond Euclid’s — which, given our statement of the dispute, would be cheating. This whole story, however, fails to address a different question about A and B — a question raised explicitly by Beltrami’s model-theoretic method, and, moreover, a type of question familiar to Locke, namely: whether A and B are even talking about the same thing. In other words, although Beltrami showed that hyperbolic “geometry” involves no logical absurdity, and is in that sense possible, he did not show that it is, even possibly, geometry. In light of this question, the point of proving the parallel postulate would not be to show that B is inconsistent, but rather to show that, when B says that two “straight lines” which intersect the same “straight line” so as to form less than two right angles on the same side may nevertheless never meet on that side, B cannot be talking about straight lines. Then this will involve exactly what looked like cheating before: namely, to make explicit whatever it is about straight lines — necessarily, something Euclid fails to say — that makes it clear that B must be changing the subject. The newly explicit constraint might take the form of a new definition of “straight line,” which will show that B’s view involves a contradiction in terms: Leibniz tries such a procedure in at least one place.[12]×See J. Heis, “Leibniz versus Kant on Euclid’s Axiom of Parallels,” pp. 11–12; De Risi, Leibniz on the Parallel Postulate and the Foundations of Geometry: The Unpublished Manuscripts (Birkhäuser, 2016, ISBN 978-3319198620), pp. 96–7. Both Heis and De Risi say that Leibniz’s proof fails, but in the text they are discussing, the In Euclidis πρῶταprōta (which is unfinished and contains many erasures and restarts) it is not even clear how many attempted proofs there are and where they begin or end. Assuming De Risi’s §7 (p. 170) contains the end of a proof, the question of whether it is successful may depend on exactly what Leibniz means by “uniform” there and in §3 (p. 168). Or it might instead take the form of a new geometrical axiom or postulate which Euclid ought to have stated and which B ought to accept, the addition of which will make B’s position untenable: this, for example, is Wallis’s procedure. Or, finally, it might state a relationship between lines and some extra-geometrical concept. For example — and this brings us back to Thābit, and to Locke — a relationship between straight lines and the motions of bodies.

Now, to be clear, I should add immediately that Thābit himself would probably not accept the qualification “extra-geometrical.” The first part of his introduction is devoted to arguing, based in part on the authority of Euclid, that motion is a legitimate geometrical concept, and مجسمmujassam, although derived from the same root as جسمjism, “body,” is the standard word for “solid” in a geometrical context, the equivalent of στέρεονstereon = solidum.[13]×E.g. Elements book 11, definition 1 begins in Arabic الشكل المجسم هو …al-šakl al-mujassam huwa: see, e.g., MS Upsala Universitetsbibliotek O. Vet. 20, fol. 157r. (This part of the Arabic Elements remains unedited.) Hence he likely believes that he is using “solid” in, as Locke would put it, “[the] acceptation … which Mathematicians use it in” (Essay 2.4.1). But, whatever Thābit may think, Locke definitely agrees with Aristotle and Kant, among many others, that the movable in space is body — corporeal substance — and hence, by definition, beyond the reach of pure mathematics, whereas “The Parts of pure Space, are immovable” (2.13.14). For Locke, then, Thābit’s axiom, if it is true, is not a purely geometrical truth, but rather expresses a relation between geometry and physics.[14]×Levi-Civita may also have been thinking about the relationship between geometry and physics when he developed the theory of parallel transport: see G. Iurato and G. Ruta, “The role of virtual work in Levi-Civita’s parallel transport,” Archive for History of Exact Sciences 70 (2016):553–66.

To return, then, to my main topic. I have already shown — or, well, anyway, asserted — that, according to Locke, the diversity of simple modes of space depends entirely on the connection between finite space and body. Suppose, then, that Thābit’s axiom expresses something evidently true about bodies, namely that the movement of their parts must look like fig. 4, or, in other words, that the lines \(BA\) and \(DZ\), in fig. 1, must be straight. Then whatever follows from Thābit’s axiom, including at least the so-called triangle postulate, will act as a constraint on the qualitative diversity of those simple modes.

In a future post I will try to explain why Locke considers Thābit’s axiom to be evidently true, and, indeed, intuitive (as opposed to demonstrative). And I will also try to show that he indeed contemplates the use of exactly that principle in constraining the possible shapes of spaces.